【インデックス投資】VIX指数とS&P500の関係について|2022年11月
甲
フリギワ
【インデックス投資】資産が倍になるまでの算式、72の法則について解説
甲
こんにちは！甲(@koublog2)です。長期投資を始めたてのころ、どれくらいの期間積み立てれば目標金額に達するのか気になりますよね。
つみたてNISAだけじゃ老後の備えが足りない気がするなぁ…
ちなみにつみたてNISAを20年間満額投資した場合のシミュレーションがこちらです。
将来の総資産額：13,700,986円
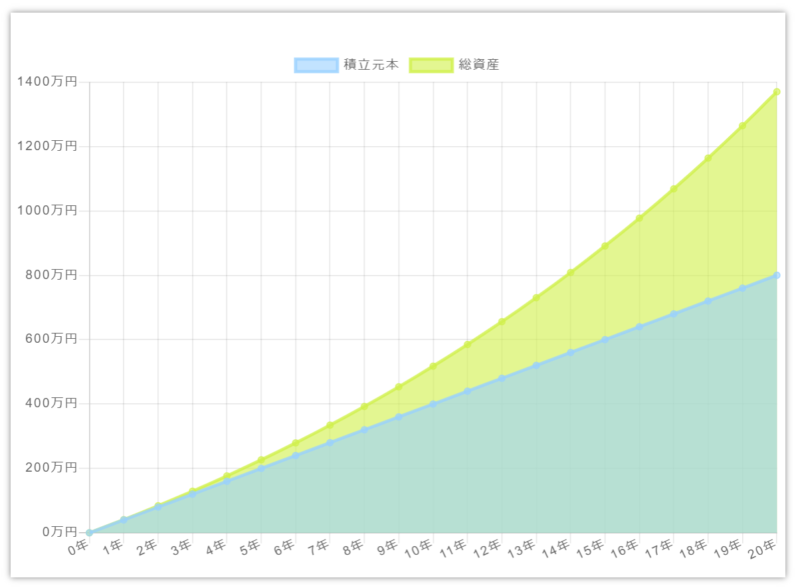
リターンは平均に近い5%としています。結果としては1370万になりました。
おそらくちょっと足りないなぁ、と感じるのではないかと思います。
積立の場合のシミュレーションは少々複雑ですが、元本が何年かければ目標金額に到達するか？
これを簡単な数式で説明されていますので紹介します。
タップできる目次
72の法則とは
結論から申し上げますと、72の法則は、お金が2倍になるまでの期間が分かる算式です。
イタリアの数学者であるルカ・パチョーリが1494年に述べたとされる数式です。500年も昔からあるんですね…
72の法則
72÷金利≒元本が2倍になるまでの期間
では、先ほど積み立てのシミュレーションを行った1370万が、倍の金額になるまでさらに何年かかるかというと
- 72÷年利5％≒14.4年
仮にリターン5%とすると、20年間かけて積み立てた1370万をさらに14年運用すれば2740万に到達します。
ただ、この72の法則はその時点の元本が2倍になるまでにどれくらいかかるか、を想定するための数式です。
仮に積立NISAで積み立てていた月33333円を、特定口座に移しても継続して積み立てた場合は、こうなります。
将来の総資産額：35,636,830円
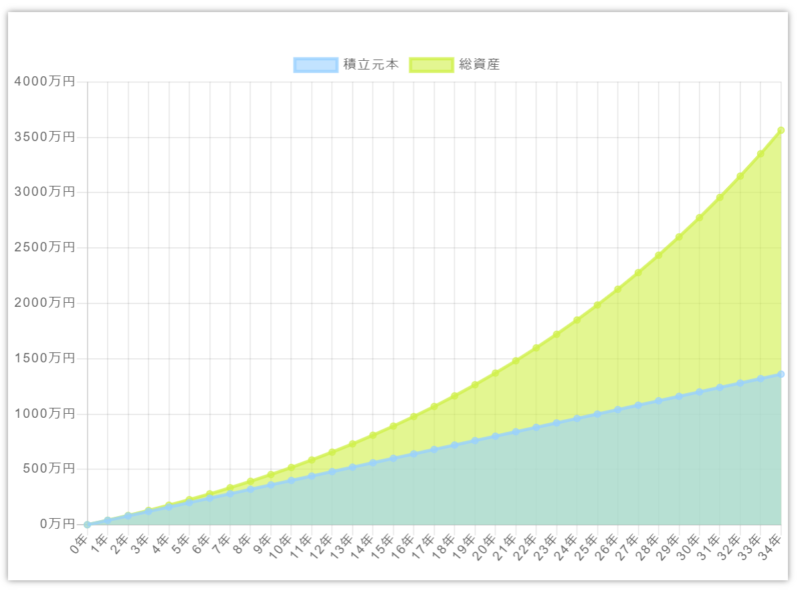
ちなみにこのシミュレーションも、72の法則も、複利の考え方で計算されています。
単利の場合、2倍になるまでの期間の計算式は、100の法則で表すことができます。
100の法則
(単利計算)
(単利計算)
100÷金利≒元本が2倍になるまでの期間
上の例にあてはめると、年利5%の場合、20年かかります。6年近く違うわけですね、
アインシュタインが
複利は人類最大の発明。知っている人は複利で稼ぎ、知らない人は利息を払う。
と言ったのも納得の結果ですね。
長期投資については以下の本で詳しく解説されていますのでお勧めです。たまに漫画も入っていて読みやすいです。
リンク
借金にも適用される72の法則
先ほど、知らない人は利息を払う、とアインシュタインが述べていることを紹介したわけですが、これが当てはまるのが借金というわけです。
仮に100万円を消費者金融で借金したとします。消費者金融での金利相場は年率18.0%だそうです。
これに72の法則を当てはめると…
72÷金利18％≒4
たった4年で借金は倍の200万です。
こ・・・こんなに借りてない！！！
と、なるわけです。
年率18%でも恐ろしいですが、法律では「利息制限法」により上限が年率20%までと定められています。
年率20%だと3年7か月で2倍です。これ以上の金利は法律違反になりますが、それでもかなり高い水準ですね。
借金がいかにおそろしいかも72の法則は教えてくれますね。
まとめ
今回は、お金が倍になるまでの期間を算出できる72の法則について解説しました。
- 72÷金利≒元本が2倍になるまでの期間
- 単利計算の場合は100の法則となる
- 72の法則は資産にも負債にも適用される法則
複利を味方につけて、入金力を高めることで目標金額までの年数を圧縮していきたいですね。
ちなみに、企業型DCでいくら積み立てるべきかについてはこちらで解説しています。
あわせて読みたい
【老後2000万問題】企業型DCでシミュレーション、結局いくら積み立てればいいの？
ということで、今日はこの辺で！それでは！
あわせて読みたい
【揺り籠から墓場まで】インデックス投資の始め方・続け方・終わり方
ABOUT ME
投資ブロガー×ファイナンシャルプランナー。つみたてNISA、企業型DC、ジュニアNISAを駆使して非課税投資をエンジョイ中。余ったお金は特定口座にも入れてます。インデックス投資や不動産クラウドファンディング、お得なキャンペーンについてブログで情報発信中。
